অনপেক্ষ বা পরম বিস্তার পরিমাপের প্রকারভেদ (Types of Absolute Measures of Dispersion)

অনপেক্ষ বা পরম বিস্তার পরিমাপ (Absolute Measures of Dispersion) হলো পরিসংখ্যানের একটি পদ্ধতি, যার মাধ্যমে ডেটাসেটের মানগুলোর মধ্যে বৈচিত্র্য বা বিচ্ছুরণ পরিমাপ করা হয়। এই পরিমাপগুলো সরাসরি মূল ডেটাসেটের একক বা মান ব্যবহার করে ডেটার মধ্যে পরিবর্তনশীলতার মাত্রা নির্ধারণ করে। এর প্রধান প্রকারভেদগুলো হলো:

১. পরিসর (Range)

সংজ্ঞা:
ডেটাসেটের সর্বোচ্চ এবং সর্বনিম্ন মানের মধ্যকার পার্থক্য হলো পরিসর। এটি ডেটার বৈচিত্র্যের একটি সরলতম পরিমাপ।

সূত্র:
Range= সর্বোচ্চ মান - সর্বনিম্ন মান

উদাহরণ:
ডেটাসেট: 5, 8, 12, 20
পরিসর: 20 - 5 = 15

গুণাবলি:

• সরল এবং দ্রুত গণনা করা যায়।
• তবে এটি কেবল চূড়ান্ত মানগুলোর উপর নির্ভরশীল, মধ্যবর্তী মান বিবেচনা করে না।

২. আন্তর্চতুর্থাংশ বিস্তৃতি (Interquartile Range)

সংজ্ঞা:
ডেটাসেটের প্রথম চতুর্থাংশ (Q1) এবং তৃতীয় চতুর্থাংশ (Q3)-এর মধ্যকার পার্থক্য হলো আন্তর্চতুর্থাংশ বিস্তৃতি। এটি মধ্যবর্তী ৫০% ডেটার বৈচিত্র্য পরিমাপ করে।

সূত্র:
IQR} = Q3 - Q1

উদাহরণ:
ডেটাসেট: 4, 8, 10, 12, 16, 20, 24
Q1 = 8 , Q3 = 20
IQR: 20 - 8 = 12

গুণাবলি:

• মধ্যবর্তী ডেটার ওপর ভিত্তি করে বৈচিত্র্য নির্ধারণ করে।
• চূড়ান্ত মানগুলোর প্রভাব কম থাকে।

৩. গড় বিচ্যুতি (Mean Deviation)

সংজ্ঞা:
ডেটাসেটের প্রতিটি মান এবং গড়ের মধ্যকার পার্থক্যের গড় হলো গড় বিচ্যুতি।

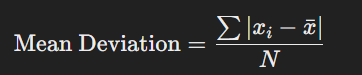
সূত্র:

যেখানে:

উদাহরণ:
ডেটাসেট: 5, 7, 9

Mean Deviation:

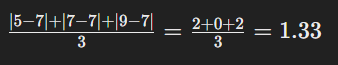
গুণাবলি:

• গড়ের চারপাশের ডেটার বিচ্যুতি পরিমাপ করে।
• ডেটার সমানভাবে বিতরণ বোঝায়।

৪. মানক বিচ্যুতি (Standard Deviation)

সংজ্ঞা:
ডেটাসেটের প্রতিটি মান এবং গড়ের মধ্যকার বিচ্যুতি (Deviation)-এর বর্গের গড়ের বর্গমূল হলো মানক বিচ্যুতি। এটি ডেটার বৈচিত্র্য পরিমাপের সবচেয়ে গুরুত্বপূর্ণ এবং ব্যাপকভাবে ব্যবহৃত পদ্ধতি।

সূত্র:

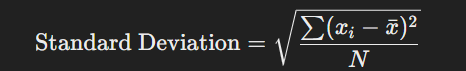
উদাহরণ:
ডেটাসেট: 6, 8, 10

Variance:

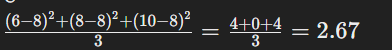
Standard Deviation:

গুণাবলি:

• ডেটার বিচ্যুতি বিশ্লেষণে সবচেয়ে নির্ভুল।
• জটিল সমস্যাগুলোর জন্য কার্যকর।

৫. বৈচিত্র্যের যোগফল (Variance)

সংজ্ঞা:
ডেটাসেটের প্রতিটি মান এবং গড়ের মধ্যকার বিচ্যুতির বর্গের গড় হলো বৈচিত্র্যের যোগফল।

সূত্র:

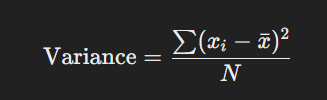
গুণাবলি:

• এটি মানক বিচ্যুতির পূর্বধাপ।
• গড় থেকে ডেটার বিচ্যুতির একটি ধারণা প্রদান করে।

সারসংক্ষেপ

অনপেক্ষ বা পরম বিস্তার পরিমাপের বিভিন্ন পদ্ধতি ডেটাসেটের ভিন্ন ভিন্ন বৈচিত্র্য বিশ্লেষণে কার্যকর। সরল পরিসর থেকে শুরু করে মানক বিচ্যুতি পর্যন্ত প্রতিটি পদ্ধতি নির্দিষ্ট প্রেক্ষাপটে ডেটার বৈচিত্র্য বা বিচ্যুতি বিশ্লেষণে সহায়ক।